Fungsi Rekursif

    Halo semua, selamat datang kembali dalam tutorial Dev-C++. Langsung saja, kali ini kita akan belajar mengenai fungsi rekursif. Pada tutorial sebelumnya kita telah belajar mengenai fungsi dan cara memanggilnya, kali ini fungsi yang akan kita pelajari kurang lebih sama dalam hal cara memanggilnya tetapi lebih cenderung banyak perbedaannya. Apa saja yang membedakan fungsi rekursif dari fungsi biasa? Mari kita simak tutorial berikut ini.

Apa itu Fungsi Rekursif?

    Pertama – tama, apa sih fungsi rekursif itu? Fungsi rekursif didefinisikan sebagai fungsi yang dapat memanggil dirinya sendiri. Jadi di dalam fungsi tersebut ada statement yang berisi nama fungsi tersebut, atau dengan kata lain perintah untuk memanggil dirinya (fungsi) itu sendiri. Nah, sekarang pertanyaannya adalah bagaimana caranya fungsi tersebut memanggil dirinya sendiri? Bagaimana mekanisme kode programnya?

Cara Menulis Fungsi Rekursif

    Cara sebuah fungsi memanggil fungsi itu sendiri adalah dengan menuliskan nama fungsi itu sendiri di dalam badan fungsinya. Penulisan nama fungsi itu sendiri dalam badan program akan menyebabkan perulangan sehingga dapat dikatakan bahwa prosesnya sama seperti perulangan (looping). Untuk lebih jelasnya mari kita perhatikan contoh fungsi rekursif di bawah ini:

    Pada program di atas, dapat kita lihat bahwa program ini memanggil fungsi void tulis() pada baris 4 yang menuliskan kalimat “Selamat datang di Fungsi Rekursif!” lalu memanggil lagi dirinya sendiri, menulis kalimat lagi, lalu memanggil lagi, terus berulang – ulang tanpa henti. Perhatikan hasil fungsi di atas berikut:

    Jadi, masalah pada fungsi di atas adalah pemanggilan tidak bisa berhenti sehingga kalimat di dalam cout keluar terus menerus! Untuk menghentikan pemanggilan, dibutuhkan yang namanya base case, yaitu statement yang berisi suatu nilai yang akan menghentikan pemanggilan fungsi. Untuk lebih jelasnya mengenai base case perhatikan contoh fungsi berikut:

    Saya memakai contoh fungsi yang sebelumnya, dan kali ini jika kalian perhatikan baik – baik saya sudah menambahkan base case pada fungsi tersebut; Pada baris 4 telah ditambahkan int x untuk menentukan berapa kali fungsi akan dipanggil, dan di dalam void tulis() terdapat fungsi if dimana fungsi akan selalu dipanggil jika nilai x > 0. Perhatikan pada baris 9, dapat kita lihat statement tersebut bahwa nilai x akan berkurang 1 setiap kali fungsi dipanggil, jadi jika nilai x sudah bernilai 0 maka di saat itulah fungsi tersebut berhenti memanggil. Untuk lebih jelasnya perhatikan gambar berikut:

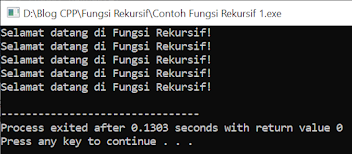
    Terlihat pada hasil program di atas, bahwa kalimat “Selamat dating di Fungsi Rekursif!” sudah tidak lagi banyak seperti hasil sebelumnya. Ini dikarenakan kode program utama int main() memanggil fungsi tulis sebanyak 5 kali, dan pada void tulis() akan mengurangi nilai pemanggilan sampai 0.

    Selain membuat fungsi rekursif yang menampilkan kalimat/string, kita juga dapat menggunakan fungsi rekursif ini untuk perhitungan matematika seperti faktorial berikut: 

• 1! = 1
• 2! = 2*1 = 2
• 3! = 3*2*1 = 6

    Dari contoh di atas dapat kita lihat bahwa untuk n = 1, jadi nilai faktorialnya dapat langsung diketahui. Maka dari itu, kita menggunakan base case-nya adalah n = 1. Perhatikanlah contoh program berikut:

    Dengan menggunakan variable n = 1 sebagai base case pada baris 7, kita dapat melihat bahwa hasil program adalah 1 dikarenakan ada return(1) pada baris 9 yang mengembalikan nilai 1. Dan pada baris 11 variabel hasil menghitung nilai n yang akan dihitung dikalikan nilai n – 1 sampai nilai n = 1, sehingga jika misalkan variable n = 3 maka perhitungan secara teori adalah 3! = 3*2*1 = 6. Saat dijalankan program di atas hasilnya akan menjadi seperti berikut:

    Untuk kasus ini saya mengisikan nilai yang ingin dihitung pada program baris 19 dengan angka 5 sehingga saat dihitung menjadi 5! = 5*4*3*2*1 dengan hasil akhirnya 120.

    Sebagai contoh berikutnya, kita akan membuat fungsi menjumlahkan kuadrat bilangan m sampai n, dengan harga awal m <= n sesuai persamaan berikut:

              Sumsq(m,n) = m²+ (m+1)²+(m+2)²+ … + n²

    Untuk persamaan di atas jika m == n maka solusi langsung didapat dengan demikian ditetapkan base case-nya adalah m==n. Coba perhatikanlah program berikut:

    Di atas adalah program untuk menjumlahkan bilangan kuadrat, pada program berikut nilai m berperan sebagai bilangan yang akan bertambah 1 setiap kali fungsi sumsq_rec dipanggil, dan nilai n akan berperan sebagai titik stop pemanggilan fungsi tersebut. Base case yang dipakai di sini adalah m==n, jadi jika kita mengisi nilai m = 2 dan n = 2, maka hasil yang didapat adalah 4 karena saat diuraikan dengan rumus fungsi di atas maka akan menjadi Sumsq_rec = 2² = 4, dan karena nilai m = n maka pemanggilan fungsi akan berhenti. Tentu saja saat kode program di atas dijalankan kita dapat memasukkan nilai m dan n sesuai yang kita inginkan. Perhatikan contoh hasil program berikut:

    Dari hasil di atas dapat kalian lihat bahwa saya memasukkan nilai m = 2 dan n = 4, dan hasil yang didapatkan adalah 29. Ini dikarenakan saat diuraikan dengan rumus fungsi Sumsq(m,n), maka akan menjadi seperti berikut:

              Sumsq(m,n) = Sumsq(2,4) = 2²+3²+4² = 4 + 9 + 16 = 29

    Ada beberapa cara untuk mendapatkan base case di atas, program di atas disebut going up recursion (rekursif naik). Cara yang lain adalah dengan going down recursion (rekursif turun), dan division in half recursion (rekursif bagi dua). Berikut saya akan terangkan fungsi rekursif turun terlebih dahulu:

    Program di atas adalah program rekursif turun, kebalikannya dari rekursif naik sebelumnya tetapi menghasilkan hasil yang sama. Yang membedakannya adalah proses perhitungan dan pemanggilan fungsi pada baris 8 dimana yang berubah adalah nilai n sedangkan nilai m tetap. Misalkan jika nilai m = 2 dan nilai n = 4 maka jika kita lihat baris 8 maka yang berubah adalah nilai n yang dihitung mundur sampai nilai n = m, sehingga hasilnya adalah sebagai berikut:

Selanjutnya, berikut fungsi rekursif bagi dua:

    Di atas adalah program fungsi rekursif bagi dua, rumus yang digunakan tetap perhitungan penjumlahan bilangan kuadrat, dengan cara pemanggilan berbeda dari kedua kode program sebelumnya. Jika kita perhatikan baik – baik pada baris 13, maka bisa dilihat bahwa fungsi sumsq_rec_3 dipanggil 2 kali untuk dijumlahkan dengan memanfaatkan variabel int mid pada baris 12. Jadi, saat dijabarkan, jika misalkan nilai m = 2 dan n = 6, maka akan dihitung terlebih dahulu variabel mid = (2+6)/2 = 4, dan hasilnya akan menjadi sumsq_rec_3(2,4) + sumsq_rec_3(5,6) = (2²+3²+4²) + (5²+6²). Berikut adalah hasil akhir perhitungan program di atas:

    Oke, kita telah selesai membahas mengenai fungsi rekursif, dan bisa disimpulkan bahwa fungsi rekursif bekerja seperti program perulangan namun terpisah, dan untuk menghentikan perulangan pemanggilan fungsi, kita harus tentukan base case-nya yang membatasi pemanggilan, dan fungsi rekursif ini juga dapat digunakan untuk menghitung operasi matematika. Demikianlah tutorial mengenai fungsi rekursif telah berakhir, semoga dapat berguna bagi kalian para pembaca. Terimakasih, dan sampai bertemu lagi pada tutorial berikutnya.